今回は統計で習った中心極限定理をPythonで可視化してイメージしてみたいと思います。
統計学の教科書とかで中心極限定理の定義は習ってざっくりとどんなものかはわかるかもしれませんが、自分で手を動かしてみるとより理解は捗るものです。
ただ、自分で手を動かして中心極限定理をやろうとすると、nを大きくする処理が必要なので、手動だと厳しいです。
というわけでPythonで簡単なコードを書きながら、中心極限定理を確認していきたいと思います。
中心極限定理とは
まずは中心極限定理を確認しておきましょう。
中心極限定理の定義はいろいろな表現がありますが、一旦こんな感じで。
このとき、確率分布の平均X_bar = (X1+X2+X3+...+Xn)/nは、nが大きい時に正規分布:N(μ, σ^2/n)で近似できる。
ここで注目したいのは、中心極限定理では元の確率分布の形は指定されていないということです。
元の確率分布が正規分布だったらそれに従う確率分布の平均も正規分布に従いそうですが、正規分布以外の二項分布やカイ二乗分布などの分布でも適用されるということです!
すごいですよね!
では次からこの処理をやっていきます。
カイ二乗分布で中心極限定理のイメージ
例としてカイ二乗分布で中心極限定理をイメージしてみます。
上でもやりましたが、正規分布だけでなくどんな確率分布でもいけるのでカイ二乗分布でもできるはずです。
ところでカイ二乗分布はどんな分布だったか確認します。
自由度5のカイ二乗分布に従うサンプルをランダムに10,000個抽出してヒストグラムを作ってみましょう。
|
1 2 3 4 |
#カイ二乗分布 df = 5 x = np.random.chisquare(df, 10000) plt.hist(x, bins = 50) |
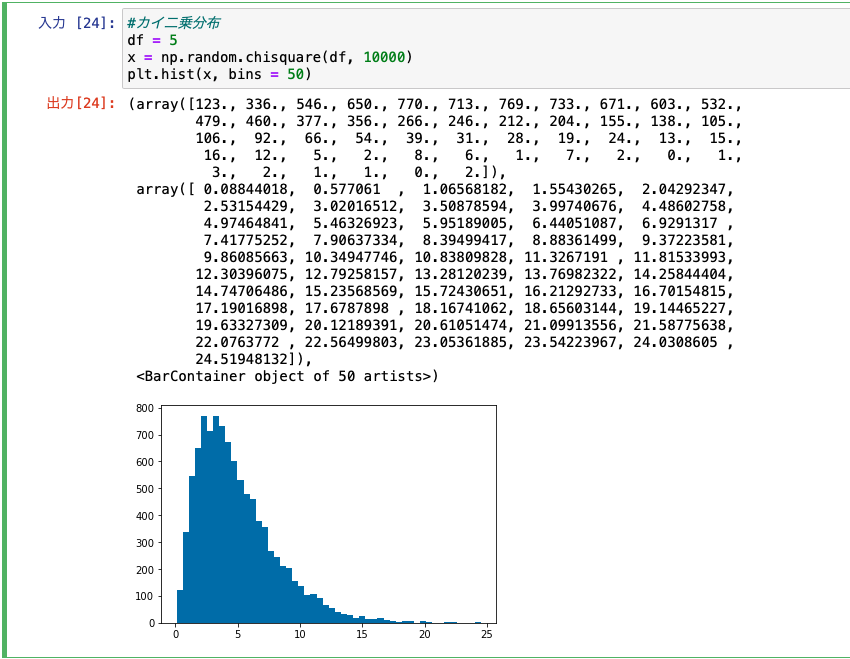
では、この自由度5のカイ二乗分布を用いて中心極限定理を考えてみましょう。
まずはこの確率分布に従う100個のサンプルを取り、それの平均を取ります(n=100の設定)。
これで平均が計算できましたが、中心極限定理を見るにはその平均の分布を確認したいので、これを1,000回繰り返してヒストグラムを作ることでその分布をみてみることにしましょう。
|
1 2 3 4 5 6 7 8 |
# 100個サンプル 1000回 chi2_list = [] for i in range(1000): sample = np.random.chisquare(df, 100) chi2_list.append(np.mean(sample)) plt.hist(chi2_list, bins = 50) |
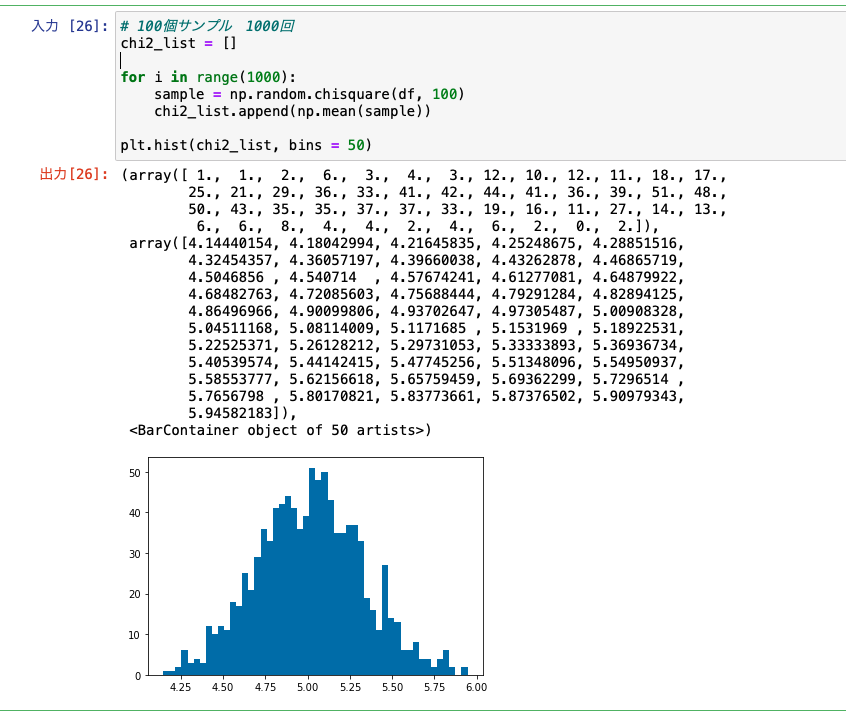
このようにカイ二乗分布から抽出したサンプルですが、だいぶ正規分布に近づいているのがわかるかと思います。
では、もっとわかりやすいように繰り返し回数を増やして10,000回にしてみましょう。
この処理は正規分布をわかりやすくするだけの追加処理です。
|
1 2 3 4 5 6 7 8 |
# 100個サンプル 10,000回 chi2_list = [] for i in range(10000): sample = np.random.chisquare(df, 100) chi2_list.append(np.mean(sample)) plt.hist(chi2_list, bins = 50) |
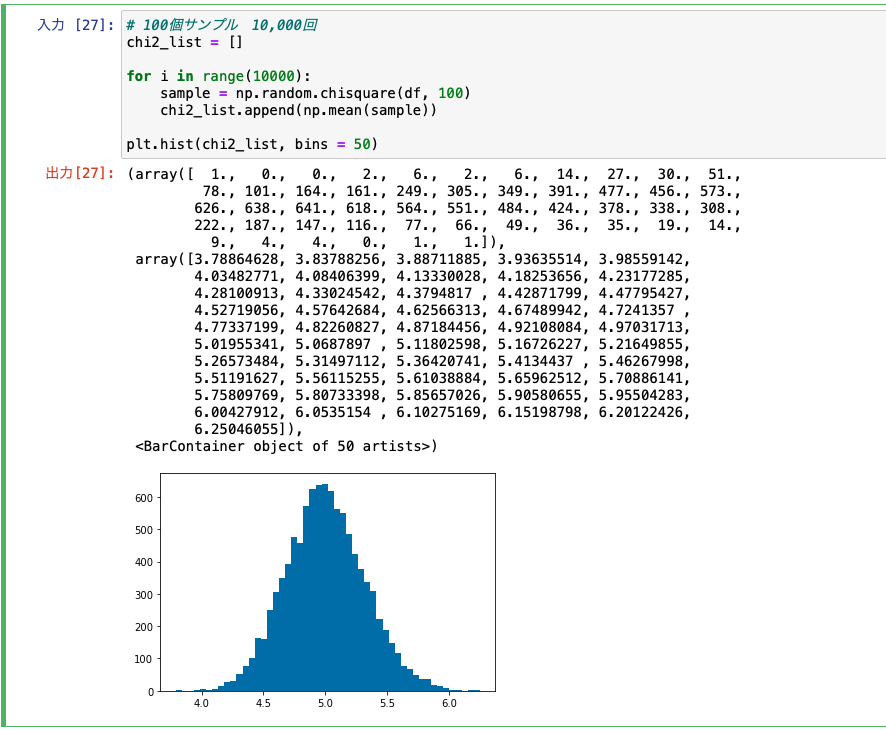
これで中心極限定理で正規分布に近づくことがわかったかと思います。
平均と分散の確認
では、さらにカイ二乗分布を元に作成した確率分布の平均と分散も計算してみましょう。
カイ二乗分布の平均と分散は自由度kのとき、平均=k、分散=2kとなります。
今は自由度5のカイ二乗分布から作成していますので、k=5です。
中心極限定理の理論では、N(μ, σ^2/n)で近似できるということですから、理論上の平均は5、分散は2*5/100=0.1くらいになるはずです。
では、コードで計算するとどうでしょうか。
|
1 2 |
print("平均:", np.mean(chi2_list)) print("分散:", np.var(chi2_list)) |
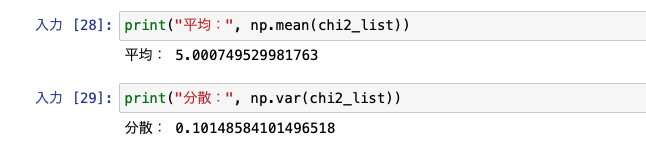
このようにほぼ平均と分散の値も理論通りになっていることがわかりますね!
こんな具合に今回はカイ二乗分布を例に中心極限定理をイメージしましたが、二項定理など別の分布でも同様のことが言えるので、興味がある方は是非やってみてくださいね!