今回は母比率の信頼区間推定をPythonでやってみたいと思います。
これまでに母平均の信頼区間推定の記事を書きましたが、母比率の方もやってみます。
母比率の信頼区間の復習
まずは母比率の信頼区間について復習しておきましょう。
そもそも信頼区間推定とは
「母比率の信頼区間の計算」は「ある母集団があり、その一部の標本から比率(割合)の範囲を推定する」というものです。
なのでこの区間推定では、「母集団からの標本」を対象にするということを理解しておく必要があります。
この記事を読めば、Pythonを使って信頼区間推定の計算はできるようになりますが、そもそもその問題背景・問題設定を理解していないと意味がありませんので注意しましょう。
あと、信頼区間では95%信頼区間などをよく使いますが、この95%信頼区間というのは平均が95%の確率でその区間に入るというわけではありません。
ベイズ信用区間などはこの考えでいいのですが、95%信頼区間といった場合には、
「母集団から標本を取り、その平均から95%信頼区間を計算する作業を100回行ったときに、95回はその区間の中に母平均が含まれるということ」です。
(統計WEB参照→https://bellcurve.jp/statistics/course/8891.html)
母平均は一つですが、標本によってはデータが変わり推定区間が変わるので、このような解釈になると思えばよいです。
母比率の信頼区間推定
まずは問題設定ですが、比率の信頼区間ということでよくあるのは確率の信頼区間を計算するものです。
ある現象が起きる確率pがあるとして、それを何回も行う状況を考えます。
この場合、確率分布は二項分布に従うわけですが、試行回数が大きい場合には二項分布は中心極限定理で標準正規分布に従うことがわかっていますね。
なので大前提として、母比率の信頼区間推定を行うときはサンプル数が大きいという条件から、二項分布を中心極限定理で正規分布に従うという仮定をおいて実施します。
そういう処理をしないとけっこう難しくなってしまうのです。
サンプル数が5とか10とかで比率を計算しようとすると厳しいです。
なので、十分サンプル数があるという状況で行うことにしましょう。
もしサンプル数が少ない状況でやらざるを得ない場合は、Clopper&Pearsonの信頼区間などを考えますが、そちらの詳細は割愛します。
では、信頼区間を二項分布を用いて考えましょう。
標準正規分布で考える場合は、下のようになりましたね。
[μ − z * σ/√n, μ + z * σ/√n]
ここで、比率なので二項分布を用いるわけですが、サンプル数が多ければ二項分布は正規分布に従うという仮定を思い出し、二項分布の場合はσ^2=p(1-p)ですから
[μ − z *√p(1-p)/n, μ + z *√p(1-p)/n]
となります。
zの値は信頼区間の%や両側・片側で値は変わってきますので、状況によって選びましょう。
最後に、母集団から標本抽出をして比率の計算ができますので、これを使って母集団の比率の信頼区間が計算できるというわけですね。
Scipyによる母比率の信頼区間推定
では、実際にScipyを使って母比率の信頼区間推定を行っていきましょう。
例題
例題は以下です。
「アンケートであるWEBサービスAを知っているか知らないかをランダムに1000人に質問した。すると、185人が知っていると答えた。このWEBサービスAの認知率の95%信頼区間を求めよ。」
Scipyコード
コードは以下のようになります。
|
1 2 3 4 5 6 |
from scipy.stats import binom n = 1000 p = 185/n #標本比率 lower, higher = binom.interval(alpha=0.95, n=n, p=p, loc=0) print("{:.2f} < x < {:.2f}".format(lower/n, higher/n)) |
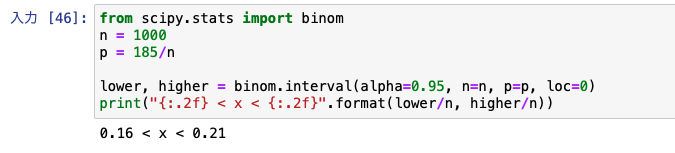
Scipyで信頼区間を計算する場合は、scipy.statsからbinomをimportします。
binomはbinomial(二項)の略ですね。
そしてサンプル数nはn=1000、確率pは1000人中185人が知っていたわけですから、p=185/1000です。
alpha引数は95%信頼区間なので0.95とします。
最終的な計算はbinom.intervalで計算するのですが、引数は確率で返されるわけではなく回数が返されるので、確率値の推定区間にするにはnで割る必要があります。
このように、binomのintervalメソッドで簡単に計算できました。
もちろんこの程度でしたら手計算でも簡単ですが、pythonコードでもできるといいですよね!
