PythonでFFT（高速フーリエ変換）〜振幅スペクトルとスペクトログラムの計算と描画

今回はPythonで高速フーリエ変換FFTをやって、振幅スペクトルとスペクトログラムの図を描いてみようと思います。

ちゃんとフーリエ変換の理論を勉強するとそれなりに大変ですが、最近は便利なものでライブラリがそろっていますから簡単に数値計算をすることができます。

FFT自体はnumpyで、スペクトログラムの作成はscipyを使ってやってみます。

簡単にできますから、ぜひ皆さんもやってみてください！

: データサイエンティストとして3年間で3社経験した僕の転職体験談まとめ

こんにちわ、サトシです。33歳です。今回は、データサイエンティストの3年間に3社で働いた僕が、データサイエンティストとしての転職活動についてまとめて書きたいと思います。これまでSE→博士研究員→ポ ...

高速フーリエ変換？FFT？

フーリエ変換は科学領域のさまざまな場面で使われますが、よくあるシチュエーションは時系列データに対して周期性があるかどうかを判定するのに使う、というものです。

この処理がフーリエ変換ですが、実際に計算機で数値計算をする場合には離散フーリエ変換を行います。

さらに、それを高速化したアルゴリズムが高速フーリエ変換（Fast Fourier Transform）で、頭文字をとってFFTと呼ばれます。

もちろん時系列データ以外にも画像解析でも使われたり、偏微分方程式の解法などでも使われますが、今回は時系列データに対する適用を考えます。

今回は理論は全て省きますので、興味ある方は次の本（Pythonで学ぶフーリエ解析と信号処理）とかを読んで勉強してみてください。

理論に加えて、Pythonでの実装も丁寧にありますので、Pythonで試してみたい方にはとても良いかと思います！

では、実際に高速フーリエ変換(FFT)をやっていきましょう！

使用するデータの確認

まずは使うデータを確認しましょう。

今回はスマホで録音した自分の声のデータを使ってみます。

声を録音した後、MP4形式からデータ分析に使える形に加工し、それをpickleファイルに入れておきました。

ちなみに「こんにちわ」と言っています。

なので、この記事ではpickleファイルを読み込むところから開始です。

pickleファイルはpandasのread_pickleを使うと一瞬で読み込んでくれます。

import pandas as pd
d = pd.read_pickle("data.pkl")
d

import pandas as pd

d = pd.read_pickle("data.pkl")

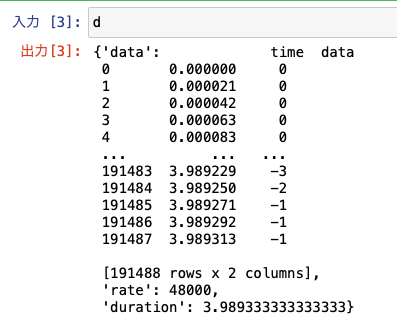
データは辞書型になっていて、キーが"data","rate","duration"の3つで、それぞれに対応する値が入っていますね。

dataが波形の値、rateがサンプリングレート、durationが継続時間です。

データを扱いやすいようにdataを読み込んで、データフレームに格納します。

df_data = d["data"]
df_data

1 2	df_data = d["data"] df_data

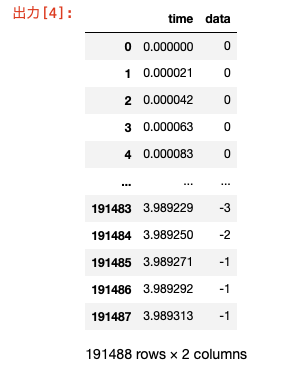
時間timeと値dataが入っています。

timeが0から4秒くらいまでで191,488行に対応するdataがあります。

ではdataを時系列に対してプロットしてみましょう！

import numpy as np
import matplotlib.pyplot as plt

data = np.array(df_data["data"], dtype=float)
time = np.array(df_data["time"], dtype=float)

plt.plot(time, data)
plt.xlabel("Time [s]")
plt.ylabel("Amplitude")

import numpy as np

import matplotlib.pyplot as plt

data = np.array(df_data["data"], dtype=float)

time = np.array(df_data["time"], dtype=float)

plt.plot(time, data)

plt.xlabel("Time [s]")

plt.ylabel("Amplitude")

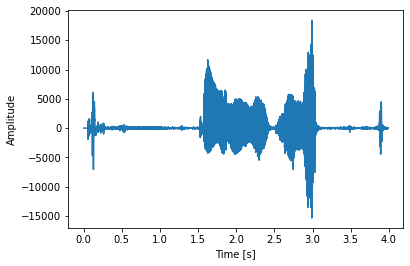
こんな感じの波形になっています。

だいたい1.5秒から3.0秒くらいで振幅が大きくなっていることがわかると思います。

rateとdurationに音声データのサンプリングレートと継続時間が入っているので確認します。

rate = d["rate"]
duration = d["duration"]

print(rate)
print(duration)

!結果================
48000
3.989333333333333

rate = d["rate"]

duration = d["duration"]

print(rate)

print(duration)

!結果================

48000

3.989333333333333

サンプリングレートは48,000Hz、継続時間は3.989秒くらいになっています。

これで使うデータの確認はOKですね！

では次からこのデータを高速フーリエ変換していきます。

Pythonのfftfreqによる高速フーリエ変換と振幅スペクトル

numpyのfftfreqでFFT

タイトルが呪文のようになっていますが、高速フーリエ変換FFTはnumpyのfftライブラリを使って計算できます。

FFTは本来データ数は2のn乗のデータ数ですから、今回は2の10乗=1024個のデータを使います。

特に今回は2秒時点から1024個のデータを使ってみます。

FFTの計算はfft.fftで計算でき、FFTの結果に対応する周波数は自分で計算してもいいですが、fft.fftfreqを使って計算できます。

FFTの結果は複素数の値になっていますので、振幅スペクトルを計算する場合はその絶対値をとります。

N = 2**10
y = data[2*rate: 2*rate + N]

F = np.fft.fft(y)
freq = np.fft.fftfreq(N, d=1/rate)

Amp = np.abs(F)

plt.plot(freq[1:int(N/2)]/1000 , Amp[1:int(N/2)])
plt.xlim(0,3)
plt.xlabel("Frequency [kHz]")
plt.ylabel("Amplitude [#]")
plt.title("FFT test")

N = 2**10

y = data[2*rate: 2*rate + N]

F = np.fft.fft(y)

freq = np.fft.fftfreq(N, d=1/rate)

Amp = np.abs(F)

plt.plot(freq[1:int(N/2)]/1000 , Amp[1:int(N/2)])

plt.xlim(0,3)

plt.xlabel("Frequency [kHz]")

plt.ylabel("Amplitude [#]")

plt.title("FFT test")

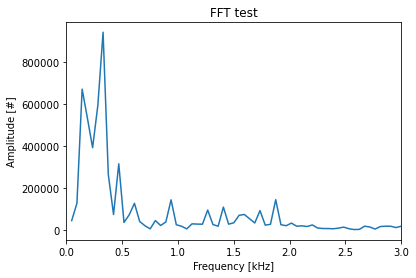
振幅スペクトルはこんな感じになりました！

0.3 kHzくらいに一番大きいピークがあることがわかりますね！

x軸のレンジは3 kHzまでにしているのでわかりづらいですが、プロットのときに配列の要素をint(N/2)までにしているのは、ナイキスト周波数までということを意味しています。

このようにnumpyのfftライブラリを使って簡単にFFTを計算して、振幅スペクトルのプロットを作ることができました。

しかし、まだ周波数に対する振幅スペクトルというグラフになっており、時間に対する変化はわからない状態です。

なので次に振幅のスペクトログラムを描いて、振幅スペクトルが時間ごとにどう変化するかわかるように描画してみたいと思います。

scipyでスペクトログラム作成

スペクトログラムはx軸が時間、y軸が周波数、z軸が色で振幅スペクトルを表します。

つまり、ある時間でFFTして振幅スペクトルを計算して縦のy軸方向に色でプロットし、次に少しずらした時間帯でFFTを計算し...ということを繰り返すということです。

普通に考えると処理を実装するのは結構めんどくさそうですが、scipyのライブラリを使うとこれまた簡単に計算することができます。

次がスペクトログラムを作るプログラムです。

import scipy.signal as signal
freqs, times, amp = signal.spectrogram(data, fs=rate, nperseg=N, scaling="spectrum")

amp[amp==0] = np.finfo(float).eps
fig, ax = plt.subplots(figsize=(12,6))
spectrogram = ax.pcolormesh(times, freqs/1000, np.log10(amp), shading="auto", vmin=0,vmax=7e0)
cbar = fig.colorbar(spectrogram, ax = ax, orientation = "vertical")
cbar.set_label("Amplitude")

ax.set_xlabel("Time [s]")
ax.set_ylabel("Frequency [kHz]")
ax.set_ylim([0, 5])

import scipy.signal as signal

freqs, times, amp = signal.spectrogram(data, fs=rate, nperseg=N, scaling="spectrum")

amp[amp==0] = np.finfo(float).eps

fig, ax = plt.subplots(figsize=(12,6))

spectrogram = ax.pcolormesh(times, freqs/1000, np.log10(amp), shading="auto", vmin=0,vmax=7e0)

cbar = fig.colorbar(spectrogram, ax = ax, orientation = "vertical")

cbar.set_label("Amplitude")

ax.set_xlabel("Time [s]")

ax.set_ylabel("Frequency [kHz]")

ax.set_ylim([0, 5])

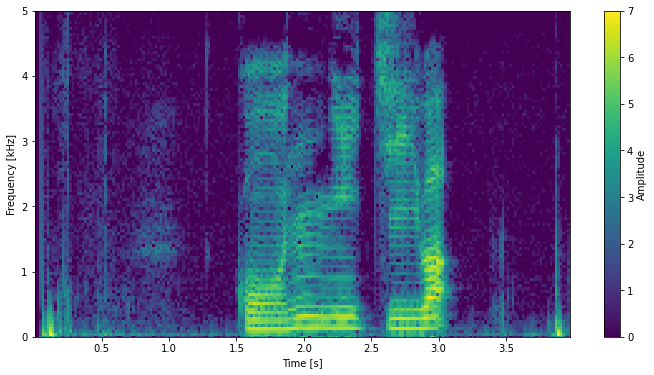
このようなスペクトログラムを作ることができました！

うまい具合にできてますね！

1.5秒から3秒くらいまでの時間帯で色が黄色くなっており、振幅スペクトルが大きくなっていることがわかると思います。

これは上の方で時系列プロットを作ったときの振幅の大きさとconsistentになっていますね！

また、上のほうに向けてシマシマがたくさんできていますが、これは高調波を表しています。

コードを見ていくと、signal.spectrogramでスペクトログラムのメインを計算します。

ただ、後々ampはlogをとるので振幅が0だと困りますので、amp=0のデータには一番小さいfloatの値finfo(float).epsを入れています。

そして、pcolormeshでz軸のカラーバーを作っています。

ちょっと描画は丁寧にやる必要がありますが、こちらもライブラリを使うと簡単に描画することができましたね！

最後に

今回はPythonで高速フーリエ変換を計算して、振幅スペクトルとスペクトログラムを描画する方法を紹介しました。

理論は少し勉強が必要ですが、計算するだけなら簡単ですね！

もしPythonとフーリエ変換をもっと詳しく学びたければ、Udemyにも講座があるので見てみるとよいかと思います。とりあえずフーリエ変換の概要理解と実装ができるようになります。

Udemy：【フーリエ変換ことはじめ】フーリエ変換を使えるようになろう

では最後まで読んでいただき、ありがとうございました！